Как рассчитывать доверительные границы к частоте и вероятности

Расширенные варианты моих статей и иллюстративных материалов

Расчет доверительных границ к частоте

Есть два разных понятия: вероятность и частота. Частота события – это наблюдаемый показатель, который определяется как n/N, где N – общее число наблюдений, а n число «успешных» наблюдений, то есть тех, в которых это событие произошло. Например, если в серии из 20 подбрасываний симметричной монетки «решка» выпала 12 раз, то частота этого события – 0,6, а вероятность – 0,5.

В принципе при любом количестве наблюдений частота и вероятность могут различаться сколь угодно сильно в пределах возможного, однако большие отклонения маловероятны, и при увеличении числа наблюдений частота будет приближаться к вероятности. Если задать р, принятую как границу между вероятными и маловероятными событиями (в медицине обычно р берут равным 0,05), то можно рассчитать границы, вне которых различия частоты и вероятности будут маловероятны.

Соответственно есть две разные задачи: определение возможных границ частоты при заданной вероятности и определение границ возможной вероятности при заданной частоте.

Пусть, к примеру, принято, что доля детей школьного возраста, больных сахарным диабетом, равна 1%. Рассчитаем, насколько вероятна та или иная частота в школе с 535 учениками.

В предположении о независимости случаев заболевания число заболевших распределено биномиально. Это распределение имеется в Excel в качестве встроенной функции. Рассчитаем распределение. Для начала введем исходные значения, заголовки колонок и минимально возможное количество больных, то есть 0:

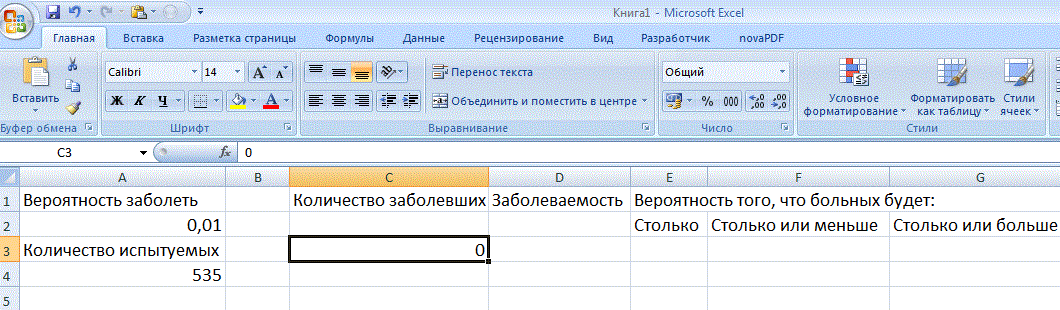
Рассчитаем заболеваемость, поделив число заболевших на число наблюдений. Так как эта формула будет копироваться, а общее число меняться не должно, то зафиксируем ссылку на него, добавив знаки доллара в ссылку:

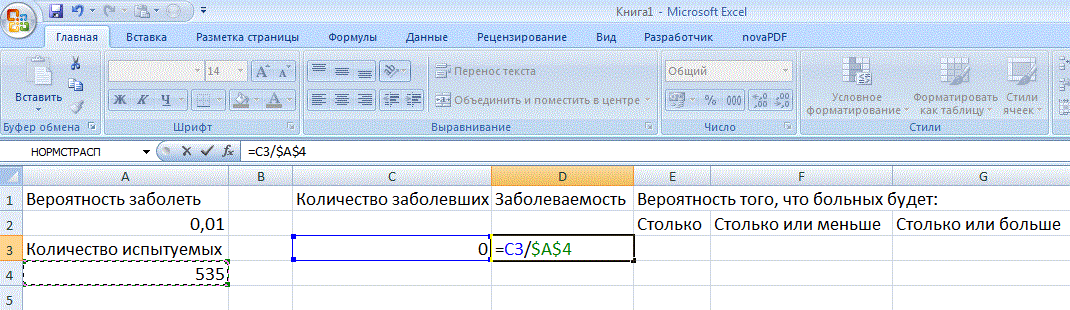
Для расчета вероятности вызовем мастера функций и выберем так функцию БИНОМРАСП. Обратим внимание на то, какие ссылки фиксируются, какие – нет:

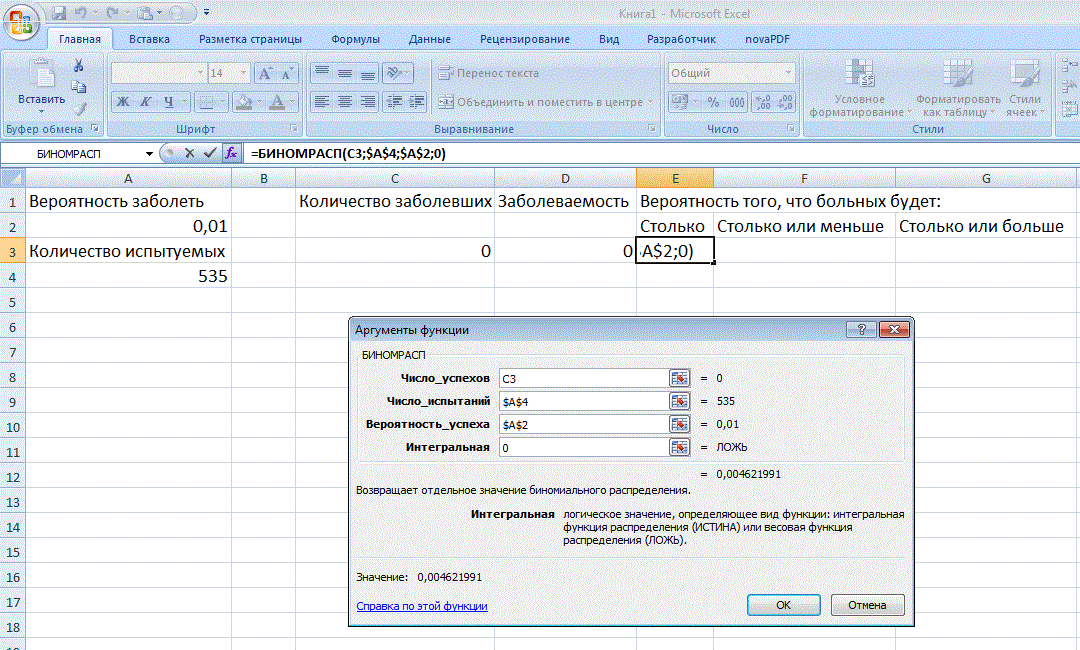
Так как меньше нуля число заболевших быть не может, то вероятность того, что заболевших будет ноль или меньше, равно вероятности того, что будет в точности ноль, а вероятность того, что будет ноль или больше, равна 1:

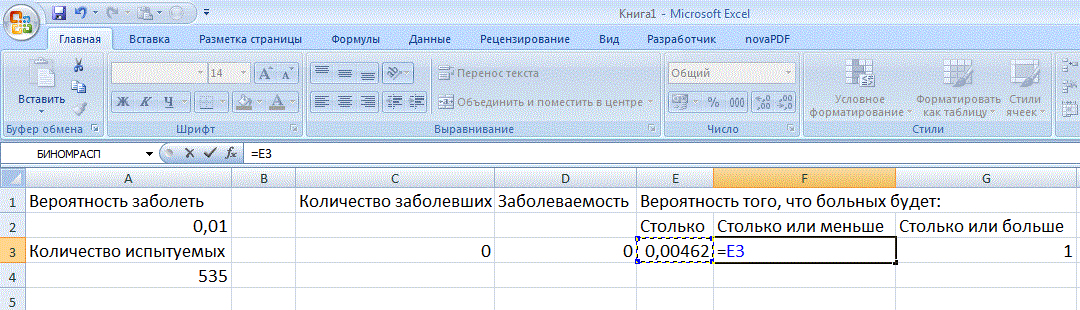
Следующее количество заболевших должно быть на 1 больше:

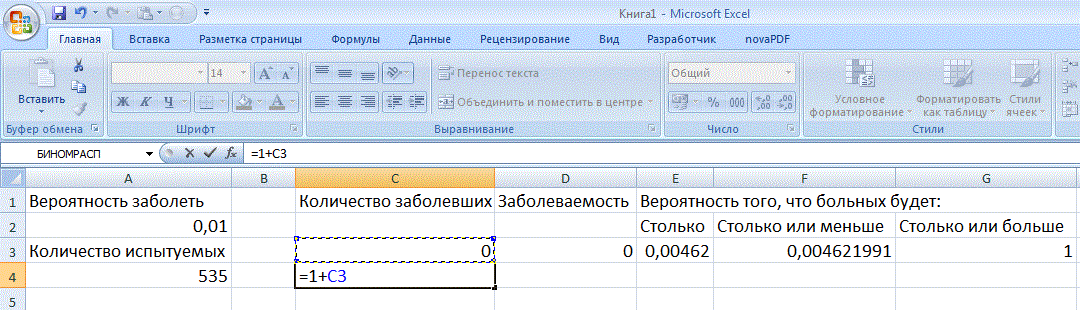
Формулы для вычисления заболеваемости и вероятности данного количества больных не меняются, поэтому выделяем эти две ячейки и копируем, «растянув» вниз за правый нижний угол:

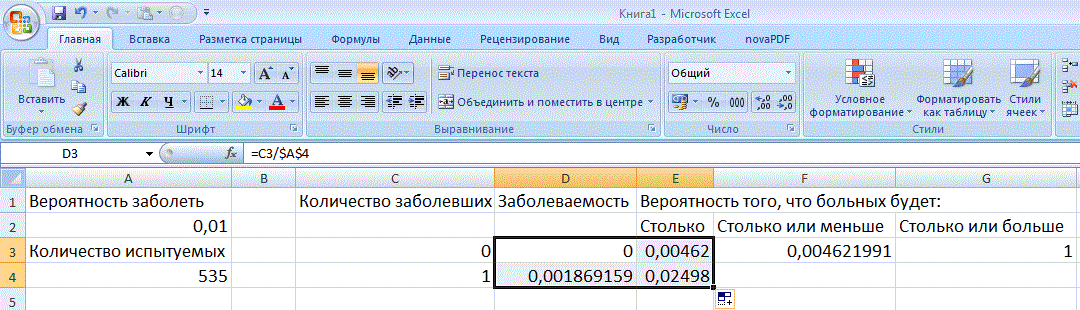
Вероятность того, что будет n или меньше больных, равна сумме вероятностей того, что будет в точности n, и того, что будет n-1 или меньше. Поэтому для вычисления следующей колонки достаточно суммировать то, что левее, с тем, что выше:

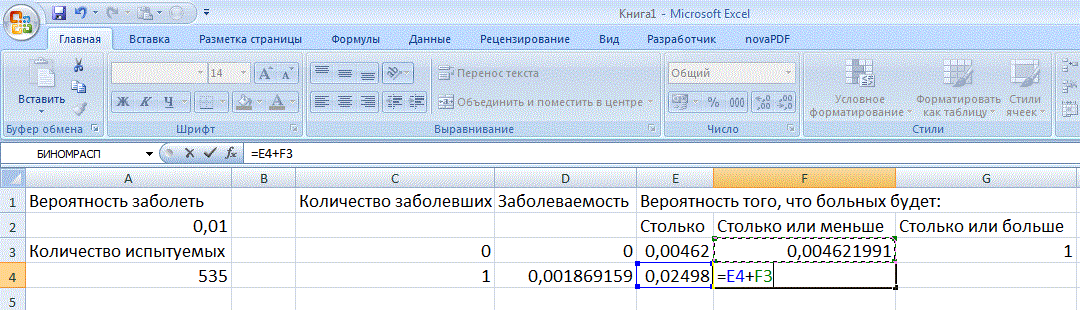
Аналогично вероятность того, что будет n или больше больных, равна вероятность того, что будет n – 1 больной, минус вероятность, того, что будет в точности n:

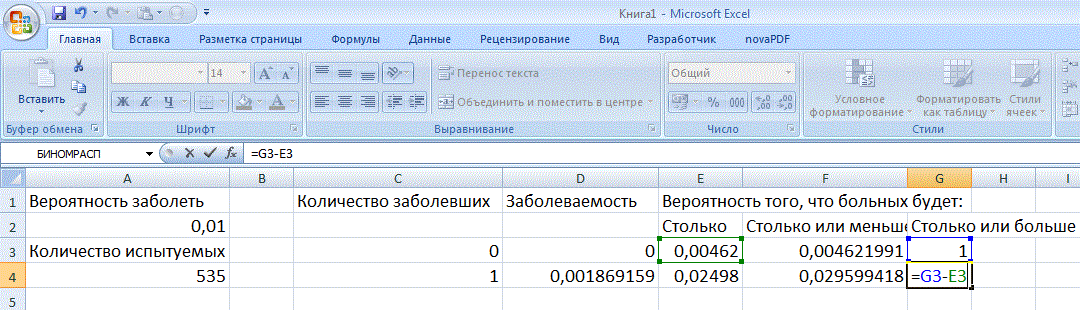
Теперь у нас имеются «эталонные» ячейки с расчетами. Выделим их и размножим, «растянув» вниз:

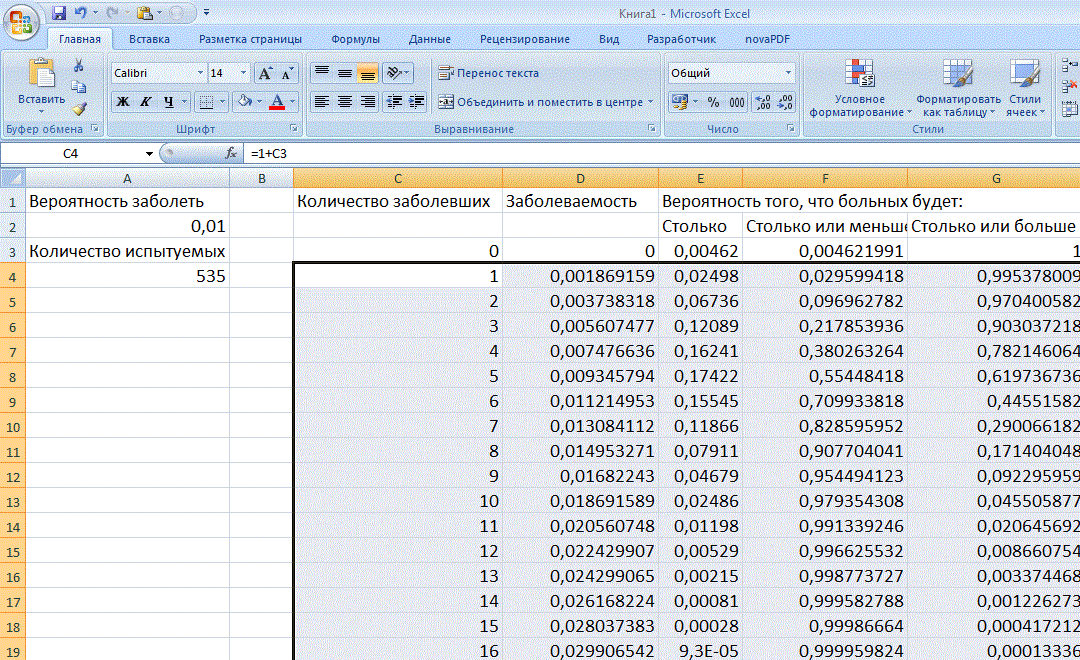
Если мы возьмем в качестве границы между возможными и маловероятными событиями р=0,05, то получим, что событие «число заболевших равно 1 или менее» будет происходить с вероятностью 0,029599…, то есть будет маловероятным, а событие «число заболевших равно 2 или менее» - с вероятностью 0,09696…, то есть это вполне вероятно. Следовательно, ожидаемое число заболевших будет 2 или более.
Вероятность того, что число заболевших будет 9 или более, равно 0,0923…, то есть при заданном р будет считаться вероятным, тогда как вероятность того, что заболевших будет 10 или более, равна 0,0455…, то есть маловероятно. Следовательно, ожидается, что число заболевших будет 9 или менее.
В результате получили, что число заболевших ожидается в пределах от 2 до 9, что соответствует заболеваемости от 0,37% до 1,68%. При этом, однако, если мы проверяем гипотезы «частота не меньше A с вероятностью p» и «частота не больше B с вероятностью p» с вероятностью р, то событие «частота находится в пределах от A до B» будет происходить с вероятностью не менее 1-2р. В результате получили, что ожидаемое число заболевших в пределах от 2 до 9 будет соответствовать 90%-ному, а не 95%-ному доверительному интервалу. Поэтому при расчете двусторонних доверительных интервалов в качестве границы между вероятными и маловероятными событиями надо брать не р, а р/2. В нашем случае 95%-ный доверительный интервал для абсолютной заболеваемости будет от 1 до 10 случаев заболевания, или с заболеваемостью от 0,187% до 1,87%.

Рассмотренная задача – определение возможных границ частоты при известной вероятности. Чаще приходится решать обратную задачу – определения возможных границ вероятности при заданной частоте. В принципе, ее можно сделать при помощи полученной электронной таблицы, проводя расчеты при разных значениях вероятности заболеть и определяя границы, в которых наблюдаемая частота будет вероятной. Однако данная процедура достаточно трудоемка, поэтому мной была создана и выложена в Интернет программа для решения рассматриваемой задачи. http://1mgmu.com/progi1/Default.aspx

Пусть, например, в школе из 535 учеников больны 5. Переходим по указанной ссылке, общее число учеников вводим как «Число наблюдений», число больных – как «Число успехов» и нажимаем на кнопку «Посчитать»:

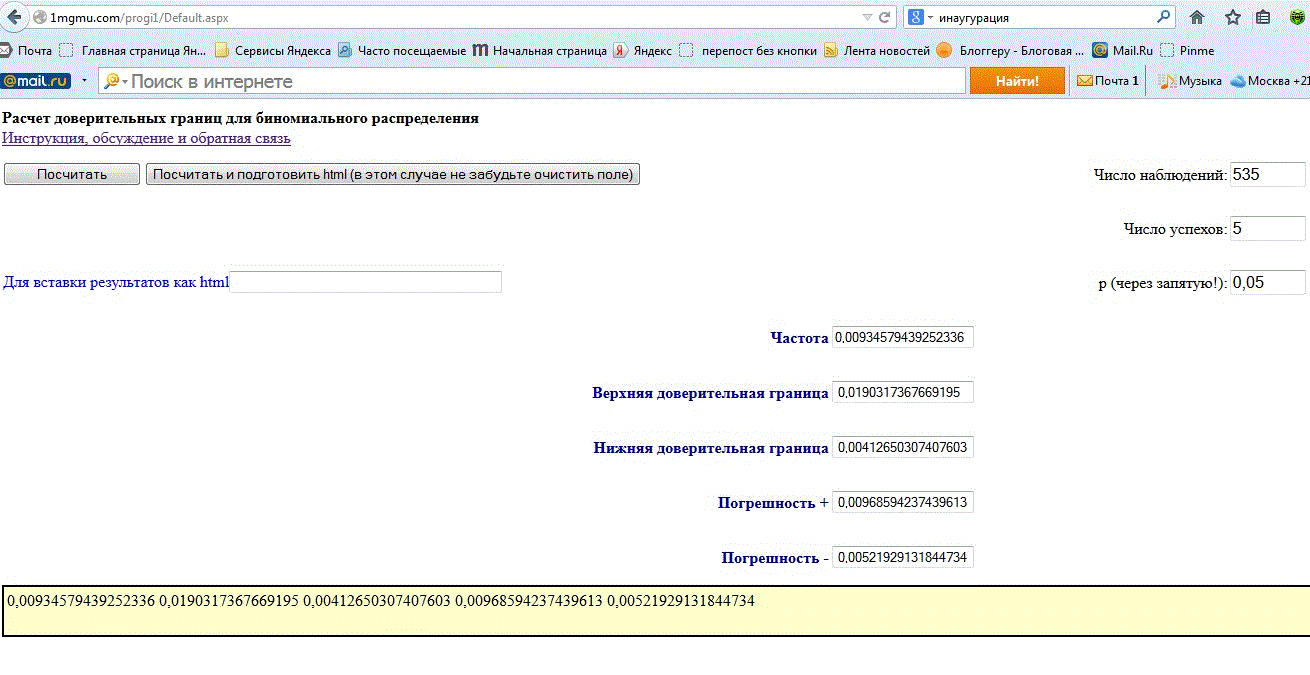
То есть получаем, что 95%-ные односторонние доверительные границы для заболеваемости – от 0 до 1,903% и от 0,413% до 100%.
Для расчета двусторонних 95%-ных доверительных границ нужно ввести р=0,025

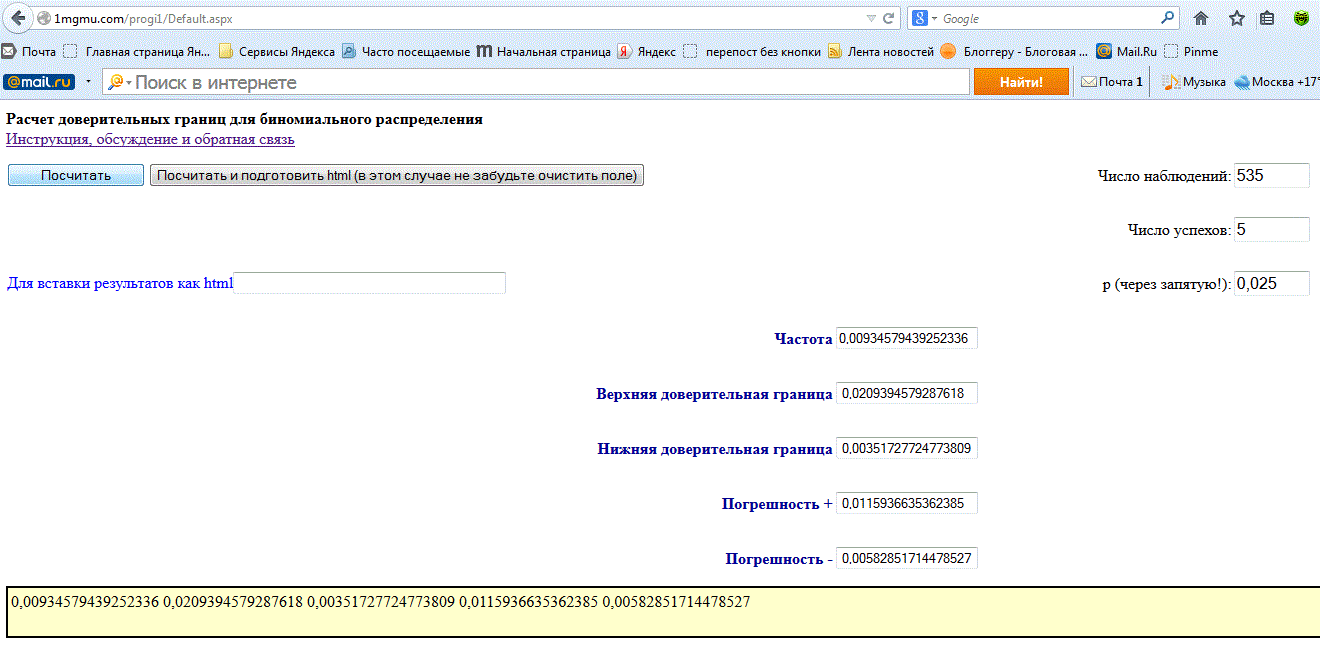
Получаем, что двусторонние 95%-ные доверительные границы - от 0,352% до 2,094%.
Рассчитанные величины можно выделить и скопировать через буфер обмена.
Подробное описание того, как использовать рассчитанные величины для построения графиков:
http://uborshizzza.livejournal.com/1316857.html

НА ГЛАВНУЮ СТРАНИЦУ САЙТА